旧地狱 part 1
date
Jul 17, 2018 → Jun 11, 2019
slug
old-blog-posts-part-1
status
Published
tags
archive
summary
type
Post
Hexo 旧博客备份(代码部分),日期升序
Hello-World-Fill-a-Vacuum-Blog-with-a-Vacuum-Track
date: 2018-07-17 23:16:47
photos: https://i.loli.net/2019/04/30/5cc8147423dd4.jpg
跌跌撞撞,我的个人小站也就算搭好了。
坐标AH scyz,目前是准高二。
高一这一年没有好好地学习OI,现在虽心有不甘,但也无所谓了。
这个blog有可能三四个月后就会暂停更新,也有可能持续更新到明年的这个时候,不过都无所谓了。
既然现在目标已经明确,就别问晚不晚。
有目标,又有这个可以分享我的观点和心情的地方,足够了。
用这首《無人区-Vacuum Track#ADD8E6》来结束我的第一篇文章吧。
十日しかないので六人合わせてBGAをとにかく完成しました。 もうすぐ締切日だから不足なところを修正する時間がない本当にごめんなさい、を許して下さい! ----passantea☆ Team:EVER BURST bga by team DSSQ Sound: Nokany BMS: Nokany Illustrator: Redo, 绝命毒师黑长直 BGA:passantea, 霸氣爺們勾, Escid, 中国龙, 马里K, LittleBitHarsh
初赛试题选讲 听课笔记
date: 2018-10-12 19:06:14
photos:
description: AFO前浪一浪- 由数字 1,1,2,4,8,8 所组成的不同四位数个数?
讨论所有以1开头的四位数。
每种组合有多少种排列方式? 排除重复元素 -> 除以元素出现次数的阶乘
- 4本不同的书A,B,C,D,其中AB是红皮的,CD是黑皮的,4本书摆在书架上...
捆绑法。
(1)把两本黑书视为整体,即求A,B,(CD)的排列 ,注意(CD)内部也有两种不同的顺序,所以答案为
(2)同理。因为A比C靠左,则两捆顺序已固定。
- 用黑白两色填涂1*8的方格,不允许两个黑格相邻。
插空法。白格至少4个,至多8个。
4白:5个空隙,插入4个黑格。
5白:6个空隙,插入3个黑格。以此类推。
$C^4_5+C^3_6+C^2_7+C^1_8+C^0_9$
- 重新排列1234使每个数字都不在原来的位置上。
错排。
我还是背公式吧
- 将6个不同的球放入3个无差别的盒子中,要求盒子非空,有几种方案?
第二类Stirling数。考虑第n+1个元素:
(1)如果n个元素构成了m-1个集合,那么第n+1个元素单独构成一个集合。方案数.
(2)如果n个元素已经构成了m个集合,将第n+1个元素插入到任意一个集合。方案数 .
所以
特殊地,
直接抄百度百科
总之,最后一个球要么独占一个盒子,要么和其他球共享一个盒子。
- 节点数为5的不同形态的二叉树有多少种?
Catalan数。设为节点数为n的二叉树数。
首先根节点一定存在。设左子树有个节点,则右子树个节点。
特殊地,
- 4个不同的点构成的简单无向图的个数?
至少3条边,至多条边。
再排除掉边数为3时不是连通图的情况。
- 1和2015之间(含),不能被4,5,6中任意一个整除的数有多少个?
容斥原理。掏出小蓝本
ddd手绘:
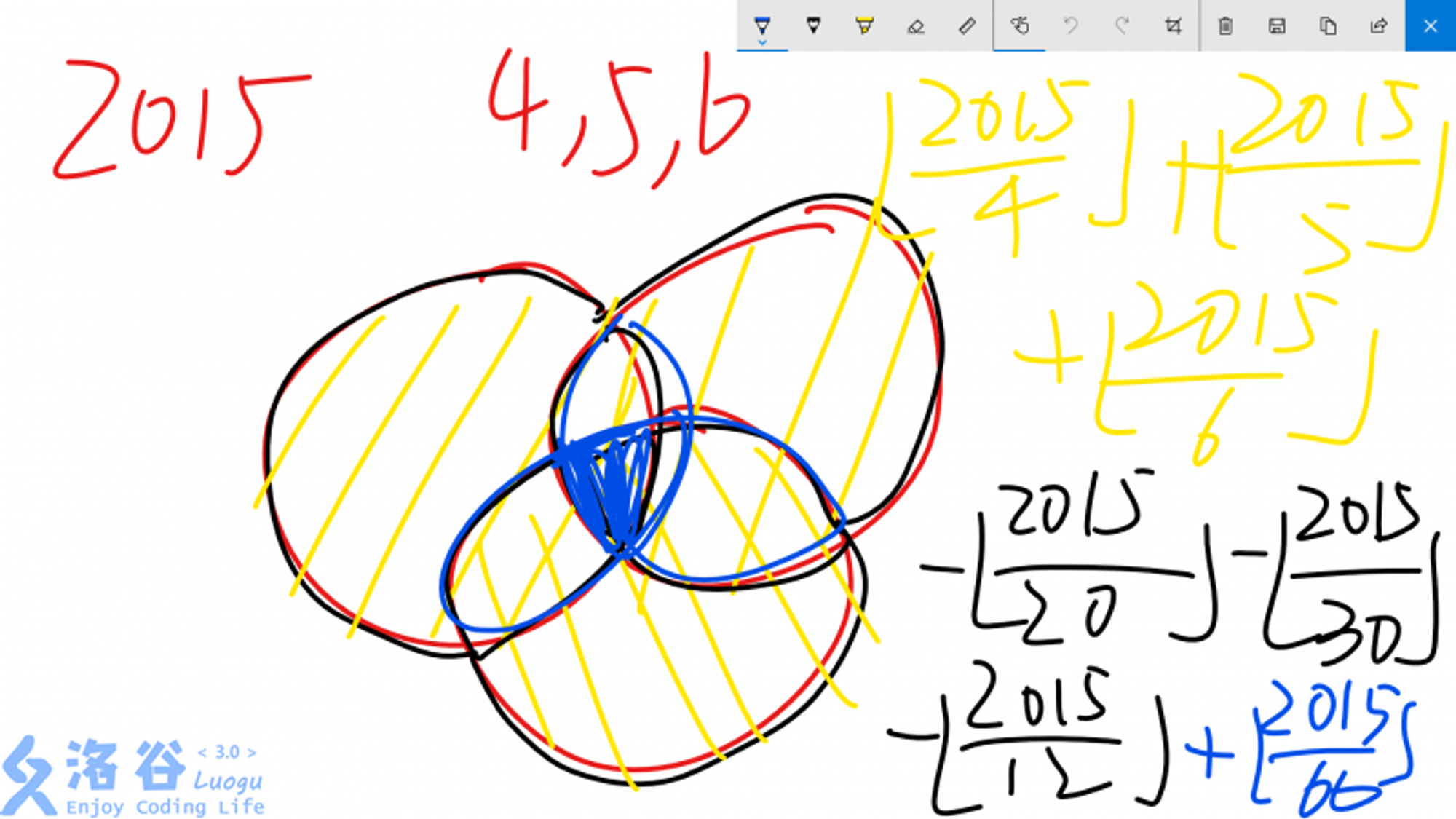
• 计算时间复杂度。
假设有递推关系式
其中
其中,为问题规模,为递推的子问题数量,为每个子问题的规模(假设每个子问题的规模基本一样),为递推以外进行的计算工作。
(1)
如果存在常数有
那么
(2)
a. Wikipedia ver.
如果存在常数$k≥0,$有
那么
b.Baidu Baike ver.
若那么
(3)
如果存在常数有
同时存在常数以及充分大的满足那么
luogu2704 [NOI2001]炮兵阵地(状压DP)
date: 2019-03-08 22:23:42
photos: https://i.loli.net/2019/04/30/5cc8141da61b6.jpg
似乎没见lg的题解有这么写的?
分析
记表示前行最后两行的状态为的时候的最大炮兵数量.
对于来说诸如
00000011、00001101的状态是根本不可能的,枚举每行时枚举到这些状态纯粹是浪费时间。
所以先找出一行内所有可行状态(get_state),这样节省了时间,还节省了空间。
开不下,而由get_state知m == 10时可行状态才只有60种,这就能开下了.代码
纸张记录
date: 2019-04-03 22:46:27
photos: https://timgsa.baidu.com/timg?image&quality=80&size=b9999_10000&sec=1555606985164&di=be984e29b16e372b7c04402bdc81c2f6&imgtype=0&src=http%3A%2F%2Fbpic.ooopic.com%2F15%2F98%2F19%2F15981982-7b44de2f1b2256153ca8573d5cb170f3.jpg
description: 记录纸张瞬间
- 字符串读入
因为buf[0]是'\0'.
luogu1144 最短路计数(最短路+"DP")
date: 2019-04-03 22:47:27
photos: https://i.loli.net/2019/04/30/5cc813da562f6.jpg
最终还是投入 $SPFA$ 的怀抱.
分析
在SPFA的过程中进行一点处理.
记为结点1到节点i的最短路条数.
①第一次发现结点x 如图中(结点2 -> 结点5)
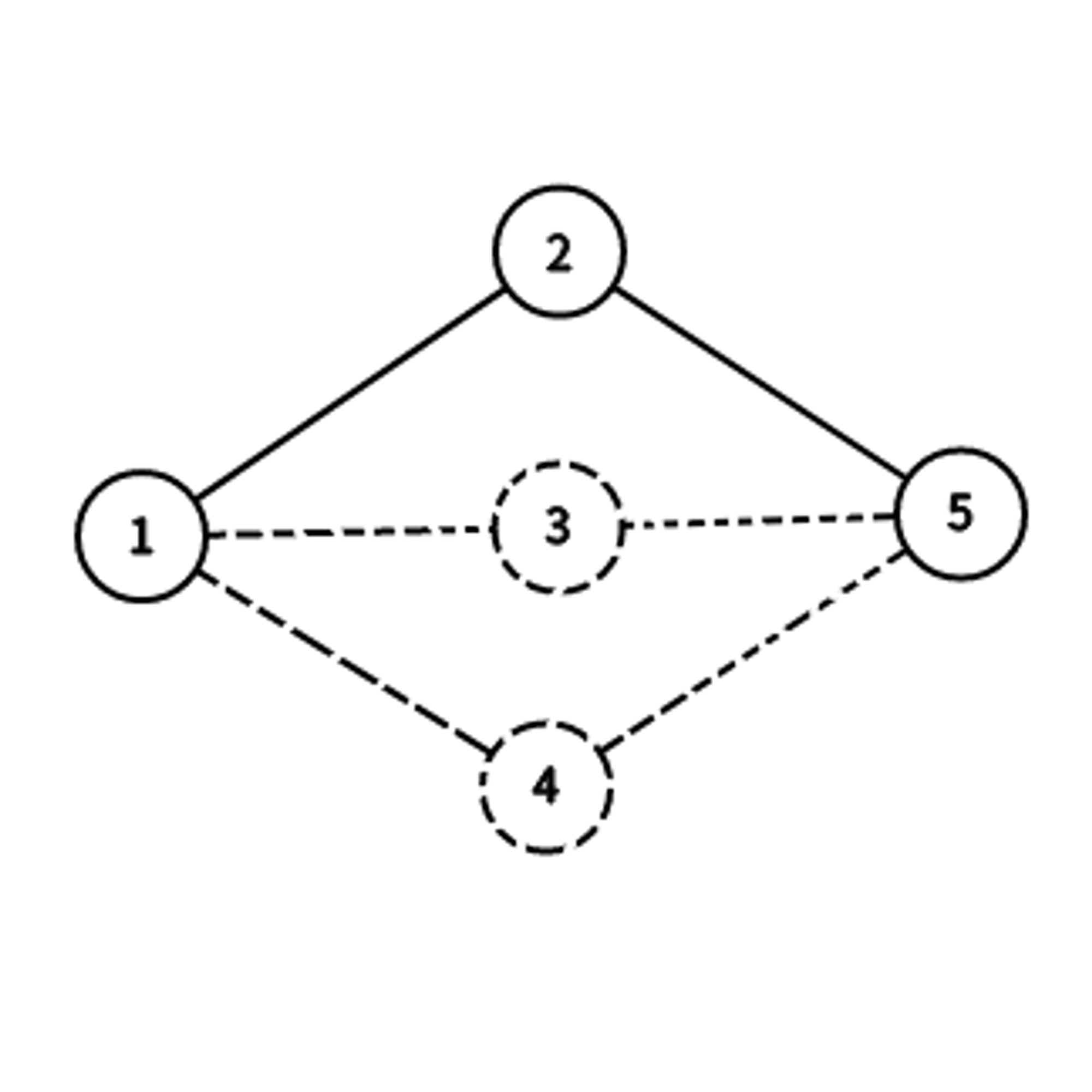
此时只能通过x的u到达x,所以.
②再次找到结点x时(结点3 -> 结点5)
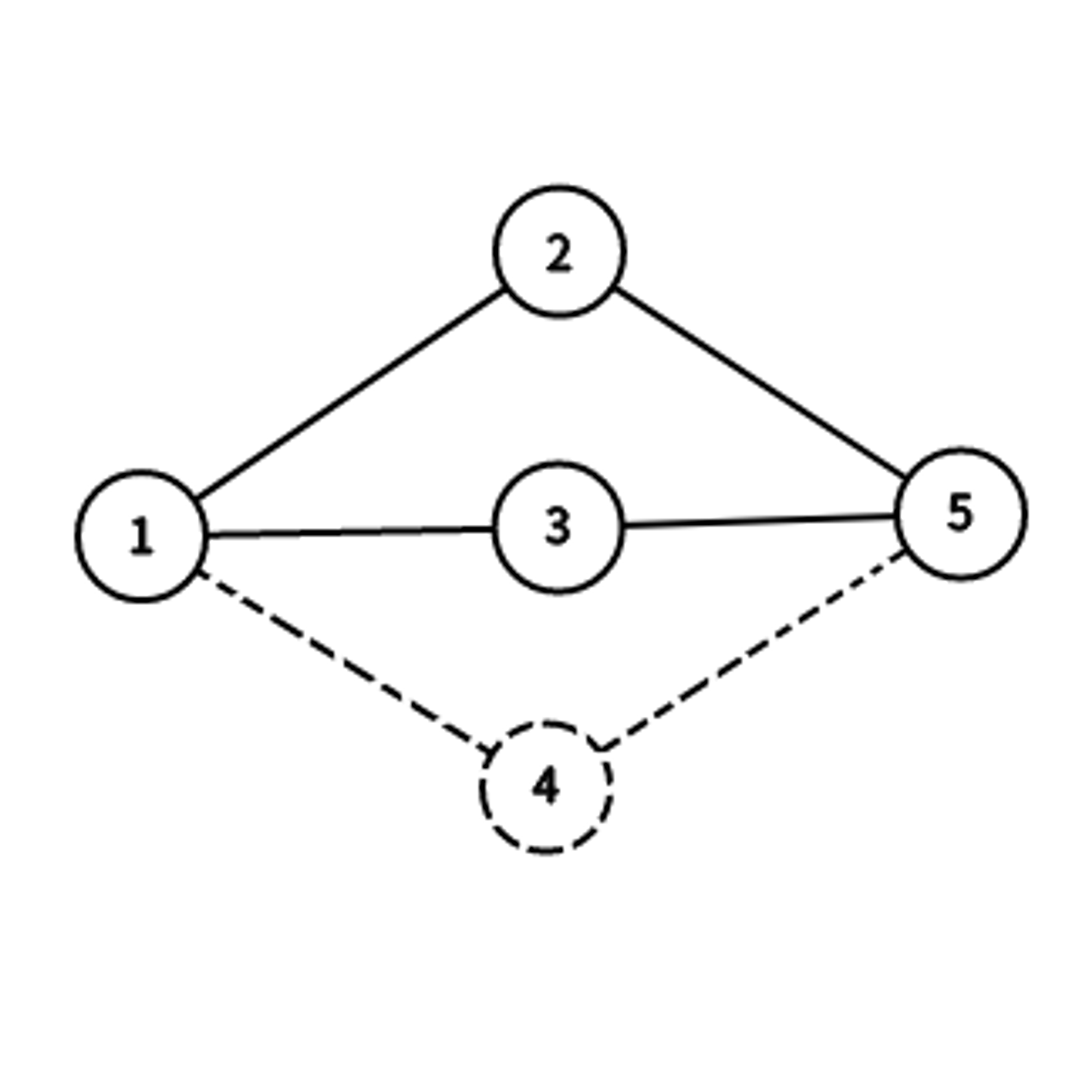
多了一条路(3 -> 5),所以.
别忘了取模!
代码
luogu3627 [APIO2009] 抢掠计划(缩点+最长路)
date: 2019-04-30 08:42:20
photos: https://i.loli.net/2019/04/30/5cc8137a9db68.jpg
藏在一堆紫黑题中的蓝题(
分析
首先想到缩点,然后统计每个强连通分量中的点权值和,建一个新图跑最长路.
一旦在原图中找到一条边连接两个分量,则在新图中连一条边.
表示分量中所有点的权值和.
求最长路可以给边权取相反数跑SPFA(即上面的连边方法),得到的结果是最长路的相反数.或者拓扑排序+DP.
注意缩点后的操作都是针对连通分量来的.
同机房 pz dalao%%%的拓扑排序+DP代码:
代码(缩点+SPFA)
luogu2814 家谱(字符串+并查集)
date: 2019-05-28 08:15:52
photos: https://i.loli.net/2019/05/28/5cec7f01ef6df89367.jpeg
这题不该是蓝的吧?(但我想了很久)
分析
用
map<string,string>存储人的名字和他祖先的名字.
输入过于毒瘤。对于这么奇怪的输入(一不小心就把人名首字母吃了)当然要用奇怪的方法(?)
详见代码.
代码
线段树模板(upd:区间乘)
date: 2019-06-04 14:58:36
photos: https://i.loli.net/2019/06/04/5cf617c83307914506.jpeg
连线段树都不会写了,我太蒻了
这里贴综合网上各种版本后写出来的板子,备忘
luogu3372 (区间加)
luogu3373 (区间乘)
CF914D (区间gcd)
感谢:
乱搞旧手机Xshell+Termux防坑记
date: 2019-06-11 16:50:19
photos: https://i.loli.net/2019/06/11/5cff6c69cb68d59487.png
未完成,xftp部分待续
没有动力写代码了就搞点别的,就有了这一篇文章(x
关于SSH,如果不是\lq老师讲课时曾经用过Xshell我都不会想到这么玩(
先放张成果图,我觉得整体体验是海星的:
字体:
PragmataProTermux是啥就不多说了,前置芝士和配置参考:
剩下的内容网上都是互相抄...开始自行摸索
记录一些踩的坑:
- vim里按下backspace键回到行首
这锅得Xshell背...
属性 - 终端 - 键盘
DELETE键序列和BACKSPACE键序列都选第二项ASCII 127似乎Windows上的gvim也会有这个问题,当时搞了半天弄不好就弃了
- 装了zsh脚本后出现的storage文件夹里啥都没有 {% fb_img https://i.loli.net/2019/06/11/5cff6e942416e76760.png %}

我怎么感觉这种方式能访问SD卡是以讹传讹...该怎么搞还怎么搞嘛,如图
{% fb_img https://i.loli.net/2019/06/11/5cff6f07c8a1888749.png %}
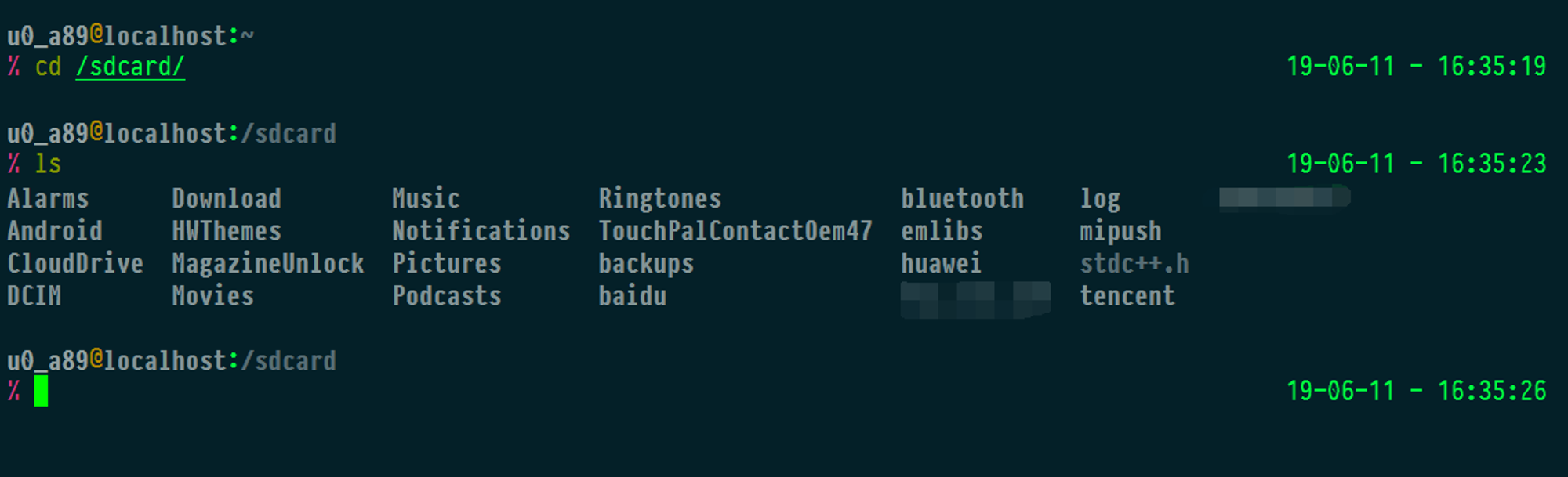
$PREFIX/include/bits/里没有stdc++.h对OI玩家极不友好手动复制一份进去
- 怎么传文件?
这玩意儿没有
rz命令(sz倒是有,喷了)不想次次都插线就用SFTP吧
- Hello World {% fb_img https://s2.ax1x.com/2019/06/11/VgJOTP.png %}
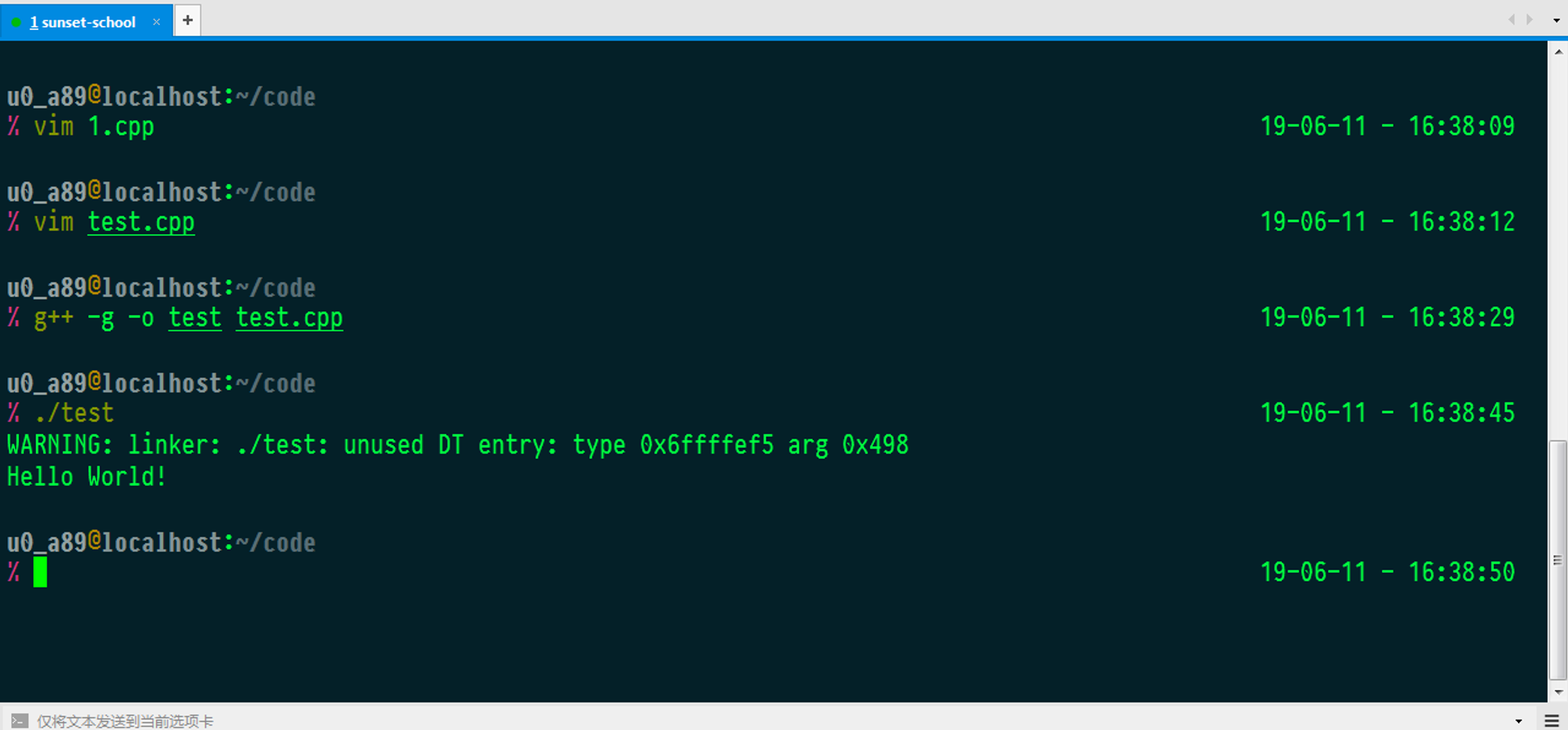
{% fb_img https://s2.ax1x.com/2019/06/11/VgJLwt.png %}
这个warning我也不知道怎么肥四啊 反正看起来没什么影响


